Erreurs et Incertitudes¶

Erreurs¶

Définition

Lors de la mesure d’une grandeur physique $X$, l’erreur est la différence entre la valeur mesurée $x$ et la valeur vraie de $X$. La valeur vraie est en général inconnue puisqu'on la cherche.

Les différents types d'erreurs de mesure.¶

Les erreurs systématiques.¶

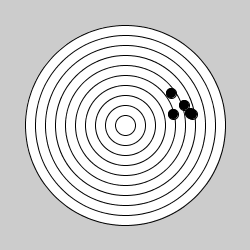
$$E_{s} = \overline{x} - x_{vraie} \quad\quad \text{avec }\overline{x}\text{ la valeur moyenne}$$

C'est une erreur qui a toujours lieu dans le même sens. Elles sont indécelables par l'analyse statistique et sont liées à la notion de justesse (écart entre la valeur moyenne observée et la valeur vraie).

Ces erreurs ont diverses origines

  • L'expérimentateur:
  • La mesure du temps à l'aide d'un chronomètre manuel introduit une erreur systématique due au temps de reflexe de l'expérimentateur.
  • La méthode de mesure: L'oubli de la poussée d'Archimède dans une pesée de précision.
  • L'appareil de mesure: Un appareil de mesure doit posséder trois qualités importantes:
    • Fidélité: diverses mesures doivent conduire au même résultat au cours du temps.
    • Sensibilité: finesse de la graduation par exemple pour les appareils de mesure analogiques.
    • Justesse:
      • L'appareil doit en outre être adapté à la mesure, il ne nous viendrait pas l'idée d'utiliser une règle pour mesurer le diamètre d'une tête d'épingle!
      • L'appareil doit aussi être utilisé correctement, l'expérimentateur doit maitriser son fonctionnement.

Les erreurs aléatoires.¶

Ces erreurs sont aléatoires, on ne peut pas en prévoir le sens. Ce peut-être tantôt une erreur en plus tantôt une erreur en moins. Si on effectue N mesures dans des conditions de répétabilité, le meilleur estimateur de la valeur vraie est la valeur moyenne $\overline{x}$ des N mesures. Mais à chaque mesure sur les N on peut avoir une différence avec $\overline{x}$. La différence est appelée erreur aléatoire :

$$E_a = x_i - \overline{x}$$

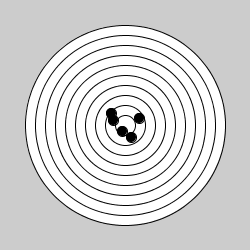
Cette variabilité est liée à la notion de précision et l'incertitude sur une mesure permet d'estimer leur importance, en supposant négligeables les erreurs systématiques.

L'origine de ces erreurs est multiples:

  • Erreur de lecture, la lecture de la position de l'aiguille d'un appareil analogique est par exemple à l'appréciation de l'expérimentateur.
  • Parasites du circuit d’alimentation en ́electronique.
  • Les conditions de mesure: température, pression, humidité doivent en toute rigueur être précisées. Elles influencent les appareils mais aussi la grandeur physique à mesurer.

Il faut donc beaucoup de rigueur et de soin pour éviter certaines erreurs fortuites.

Exemple : Commenter les figures ci-dessous en fonction du type d'erreur commise. Puis dessiner une image contenant un type d'erreur non représentée.

Erreurs : Erreurs : Erreurs :

Incertitudes¶

L’incertitude traduit les tentatives scientifiques pour estimer l’importance de l’erreur aleatoire commise. En absence d’erreur systematique, elle definit un intervalle autour de la valeur mesurée qui inclut la valeur vraie avec un niveau de confiance déterminé.

Différents modes d’évaluation de l’incertitude sur une grandeur¶

Le mot incertitude signifie doute ; l’incertitude du résultat d’un mesurage reflète l’impossibilité de connaître exactement la valeur du mesurande.

Incertitude-type de type A : par les méthodes statistiques¶

Le traitement statistique est basé sur la répétition des mesures d'une grandeur $X$. Dans la pratique, on réalise un nombre fini $N$ de mesures, de résultats respectifs $x_1, x_2,\dots, x_n$ dont on cherche à extraire les meilleures estimations de la moyenne et de la variance ou écart-type.

Les résultats des mesures effectuées de la grandeur $X$ doivent être présentés sous la forme :

$$\boxed{X = x \pm \Delta x}$$

Définition : Centre d'une distribution

On dit qu’on a une évaluation de type A de l’incertitude-type si une grandeur est estimée par des moyens statistiques. On notera ($x_1, x_2,\dots, x_n$) un n-échantillon de $X$, où $x_i$ représente la variable aléatoire associée à la $i^{\text{ième}}$ mesure de la gradeur $X$.

  • La meilleur estimation du résultat de la mesure est donnée par la moyenne arithmétique
$$\overline{x} = \dfrac{1}{n}\sum_{i=1}^{n} x_i$$

Définition : Dispersion d'une distibution

Il s'agit d'estimer ce que nous pourrions aussi appeler la largeur d'une distribution. La grandeur la plus simple à déterminer est l'étendue, différence entre les valeurs maximale et minimale. Mais celle-ci est très sensible aux valeurs extrêmes qui ne sont pas toujours représentatives, et peuvent même parfois être absurdes. D'ou l'utilisation de l'écart type.

  • L'écart type expérimental a pour expression
$$\sigma_{exp}(X) = \sqrt{\dfrac{1}{n-1}\sum_{i=1}^{n}(x_i - \overline{x})^2} = \sqrt{\dfrac{n}{n-1}(\overline{x_i^2}-\overline{x}^2)}$$

Loi de distribution :

Il faut assortir le résultat de la moyenne d’une incertitude type $u(x)$. Les mesures indépendantes de la grandeur X se distribuent selon une loi mathématique appelée loi de distribution gaussienne ou loi normale $f(x)$ donnée par la représentation graphique suivante:

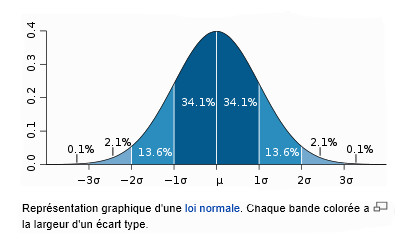
La loi de distribution définie par la fonction $f$ nous permet de connaître la probabilité que la grandeur X soit comprise dans un intervalle donné. Par exemple la probabilité de trouver la grandeur $X$ dans l'intervalle [$\overline{x}-\sigma, \overline{x}+\sigma]$ est de $68,2 \%$

  • Intervalle de confiance Dans l’hypothèse où toute erreur systematique a été ecartée et où les mesures individuelles $x_i$ sont reparties selon une loi gaussienne
$$\Delta(x) = t_{n,p\%}\times\sqrt{\dfrac{1}{n}}\times \sigma_{exp}(X) = t_{n,p\%}\times\dfrac{\sigma_{exp}(X)}{\sqrt{n}} = t_{n,p\%}\times u(x)$$

$t_{n,p\%}$ est appelé coefficient de student dependant du nombre n de mesures et du degré de probabilité souhaité (p%).

\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline n & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\\hline t(n, 95\%) & 4,30 & 3, 18 & 2, 78 & 2, 57 & 2, 45 & 2,37 & 2,31 & 2,26 & 2,23 & 2,20 \\\hline t(n, 99\%) & 9, 93 & 5, 84 & 4, 60 & 4, 03 & 3, 71 & 3,50 & 3,36 & 3,25 & 3,17 & 3,11 \\\hline \end{array}

Exercice 1 :

\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline indice & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 \\\hline X & 11 & 9 & 10 & 14 & 11 & 8 & 9 & 12 & 7 & 8 & 8 & 9 & 11 & 14 & 10 & 9 \\\hline \end{array}

Calculer :

  • La moyenne
  • L'écart type

Exercice 2 :

Pour huit maison d'un même modèle nous mesurons les résistances thermiques $R = \dfrac{\Delta T}{\Phi}$. Nous obtenons les valeurs suivantes en mK/W

\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline R & 39 & 41 & 41 & 43 & 41 & 37 & 39 & 39\\\hline \end{array}

remarque : La résistance thermique quantifie l'opposition à un flux thermique entre deux isothermes ( $T_{1}$ et $T_{2}$) entre lesquels s'échange un flux thermique $\Phi$

  1. Déterminez la valeur moyenne $\overline{R}$
  2. Calculez l'écart-type $\sigma$ de R
  3. Avec une confiance de 95%, quelle est l'incertitude $\Delta R$ ?
In [1]:
mesures = [39, 41, 41, 43, 41, 37, 39, 39]
def moyenne(mesures):
    
    
    
    
    
    
    

moyenne(mesures)
Out[1]:
40
In [3]:
from math import sqrt
def ecart_type(mesures):
   
    
    
    
    
    

ecart_type(mesures)
Out[3]:
1.8516401995451028
In [4]:
def incertitude_type(Et, n):
    return Et/sqrt(n)

deltaR = 2.37*incertitude_type(ecart_type(mesures), len(mesures))
print(deltaR)

1.55152919958

Que signifie ces résultats ?

$\sigma_{exp}$ est le paramètre qui caractérise la dispersion des valeurs $x_i$ et caractérise donc l'incertitude sur une mesure. Si on effectue $n$ mesures, $\overline{x}$ est une moyenne parmi tant d'autres (on peut répéter $m$ fois l'expérience avec $n$ mesures et on aurait $m$ moyennes). La théorie montre que que la distribution de l'ensemble des moyennes est bien moins dispersée que l'ensemble des mesures uniques (elle est divisée par $\sqrt{n}$).

Dans le cas où l'on effectue une moyenne sur un petit nombre de mesure $\sigma_{exp}$ n'est pas un bon estimateur de l'écart-type et la théorie montre qu'il est plus approprié d'utiliser l'incertitude-type $u(x)$.

À retenir, si on réalise $n$ mesures de $x$, avec les résultats $x_1 , x_2 ,\dots x_n$ , on écrira le résultat final sous la forme :

$$x = \overline{x} \pm t_{n,p\%}\times\dfrac{\sigma_{exp}(X)}{\sqrt{n}} = \overline{x} \pm t_{n,p\%}\times u(x) = \overline{x} \pm \Delta x$$

où $\overline{x}$ et $u(x)$ sont les meilleurs estimateurs de la valeur vraie et de l'incertitude-type de la mesure de la grandeur $X$

Incertitude-type de type B : On fait une mesure unique¶

Le résultat de la mesure est la valeur obtenue lors de la mesure.

Incertitude-type¶

Dans ce cas il faut prendre en compte la précision $\Delta$ de l'appareil :

  • La mesure est lue sur un appareil à graduation et on considère la valeur de $\Delta$ égale à une demi graduation. Un appareil à aiguille de classe p signifie qu’il introduit une incertitude relative de $p\%$ sur une mesure égale au calibre.

Exemple : un appareil de classe 2 comportant 150 divisions introduira une incertitude absolue de $\dfrac{2}{100}\times 150$ soit 3 divisions et ceci quelle que soit l’amplitude de la déviation.

  • La mesure est lue sur un appareil numérique et il faut lire la notice constructeur. La précision d'un appareil dépend de la résolution de l'appareil, de la qualité des composants, la précision des références de tension et de temps etc.… La précision d'un appareil numérique est généralement donnée en pourcentage de la lecture pour chaque gamme. Les appareils portatifs courants ont des précisions variant de 0.1% a 1% de la lecture suivant la gamme et la grandeur mesurée, et dans la plus part des cas a une ou deux unités (ou digits) prés.

Exemple : gamme 2 V ; Résolution 1 mV ; précision $\pm 0.1\% + 2 $ dgt ; lecture $1.000\, V$
La précision de cette mesure sera $\Delta = 0.1\%*1V+2*1 mV=3mV$).

Exemple de notice d'un multimètre bon marché

Une fois la précision $\Delta$ déterminée, l’incertitude-type sera calculée par une des lois suivantes :

  • loi normale : correspondra aux situations où le mesurande est influencé par un grand nombre de variables aléatoire et indépendantes entre elles
  • loi uniforme (rectangulaires) : affichage numérique
  • loi triangulaire : affichage analogique (cadran à aiguille)

loi normale $u(x) =\dfrac{\Delta}{3}$ : loi uniforme $u(x) =\dfrac{\Delta}{\sqrt{3}}$ : loi triangulaire $u(x) =\dfrac{\Delta}{\sqrt{6}}$

Le calcul de l'incertitude élargie et l'affichage des résultats restent sur le même principe. Avec uun niveau de confiance de $95\%$ et une loi uniforme : $$\Delta x = 2u(x) = \dfrac{2\Delta}{\sqrt{3}}$$

  • Prise en compte de plusieurs incertitudes sur une même grandeur

La mesure d'une grandeur $X$ peut-être entachée de plusieurs incertitudes. Par exemple lors d'une mesure à la règle en dehors de l'incertitude liée à la graduation $u_1(x)$ il peut y avoir une incertitude liée au positionnement de la règle $u_2(x)$. Dans ce cas les résultats statistiques montrent qu'un bon estimateur de l'incertitude type peut s'écrire :

$$u^2(x) = u_1^2(x) + u_2^2(x)$$

De manière générale s'il existe $p$ sources d'incertitudes on écrira :

$$u(x) = \sqrt{\sum_{j=1}^p u_j^2(x)}$$

Incertitude-type composée sur plusieurs grandeurs¶

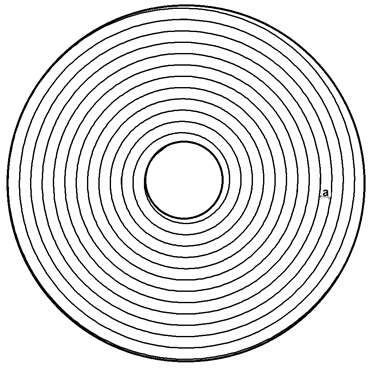
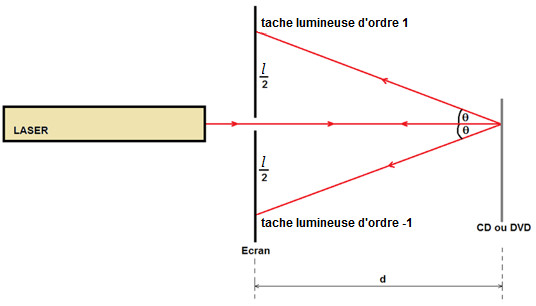
Prenons tout de suite un exemple, la mesure du pas (notée $a$) d'un disque optique à l'aide du phénomène d'interférence est liée aux mesures de deux grandeurs différentes :

Soient $d = d_m \pm \Delta d_m$ et $\ell = \ell_m \pm \Delta\ell_m$

Dans ce cas on parle de mesure indirecte. La valeur de la grandeur $a$ n'est pas accessible directement avec un appareil de mesure. Par contre on peut calculer cette valeur à l'aide d'une relation entre les différentes grandeurs.

\begin{equation} a = \lambda\sqrt{1 + 4\left(\dfrac{d}{\ell}\right)^2} \quad\quad\quad \text{(1)} \end{equation}

Les valeurs de $l$, $d$ et $\lambda$ vont être responsables d'une incertitude sur la mesure de $a$.

Propriété :

Si $Y = f(X_1, \dots, X_n)$ avec $X_1,\dots ,X_n$ indépendantes alors :

$$u^2(Y) = \sum_{i=1}^{n}\left(\left(\dfrac{\partial f}{\partial x_i}\right)^2u^2(x_i)\right)$$

Si nous appliquons ce résultat (formule de Taylor Young à l'ordre 1) à la relation précédente que l'on peut exprimer sous la forme :

$$ a = f(d, \ell)\quad\quad \text{avec les mesures $d$ et $\ell$ indépendantes}$$

On obtient :

$$u^2(a) = \left(\dfrac{\partial f}{\partial d}u(d)\right)^2 + \left(\dfrac{\partial f}{\partial \ell}u(\ell)\right)^2$$

Il nous faut maintenant exprimer la dérivée partielle pour chaque variable :

$$\dfrac{\partial f}{\partial d} = \dfrac{8\,\lambda^2\,d}{2\,a\,\ell^2}$$


$$\dfrac{\partial f}{\partial \ell} = -\dfrac{8\,\lambda^2\,d^2}{2\,a\,\ell^3}$$

Il n'y a plus qu'à écrire notre incertitude type sur $a$:

$$u(a) = \left(\dfrac{4\,\lambda^2\,d}{a\,\ell^2}\right)^2u^2(d) + \left(-\dfrac{4\,\lambda^2\,d^2}{a\,\ell^3}\right)^2u^2(\ell)$$


$$u(a) = \dfrac{4\,\lambda^2\,d^2}{a\,\ell^2} \sqrt{\left(\dfrac{u(d)}{d}\right)^2 + \left(\dfrac{u(\ell)}{\ell}\right)^2}\quad\quad (2)$$

Application numérique :

  • Connaissant $\Delta d_m$ et $\Delta \ell_m$ on calcule $u(d)$ et $u(\ell)$, avec un intervalle de confiance donné, puis avec la relation $(2)$ on calcule $u(a)$ et enfin $\Delta a_m$ toujours avec le même intervalle de confiance. Par exemple pour un intervalle de confiance à 95% : $\Delta a_m = 2\times u(a_m)$
  • Avec les mesures de $d_m$ et $\ell_m$ on calcule $a_m$ à l'aide la relation $(1)$
  • Pour finir, on exprime la grandeur mesurée sous la forme $a = a_m \pm \Delta a_m$

La propagation des incertitudes décrites par la formule précédente devient particulièrement simple dans les cas particuliers suivants :

  • Somme et différence : lorsque la grandeur n'est constituée que de sommes et de différences
$$u^2(x) = u^2(a_1) + u^2(a_2) + \dots + u^2(a_n)$$
  • Produit et quotient :
$$Y = \dfrac{x_1\,x_2}{x_n}\times\dots\quad\quad \left(\dfrac{u(Y)}{Y}\right)^2 = \left(\dfrac{u(x_1)}{x_1}\right)^2 + \left(\dfrac{u(x_2)}{x_2}\right)^2 + \dots + \left(\dfrac{u(x_n)}{x_n}\right)^2$$
  • Produit de puissance :
$$Y = x_1^\alpha\,x_2^\beta\,\dots\,x_n^\gamma\quad\quad \left(\dfrac{u(Y)}{Y}\right)^2 = \left(\alpha\dfrac{u(x_1)}{x_1}\right)^2 + \left(\beta\dfrac{u(x_2)}{x_2}\right)^2 + \dots + \left(\gamma\dfrac{u(x_n)}{x_n}\right)^2$$

Exemples :

  • La période d'oscillation d'un pendule simple dépend de la longueur du pendule $$T = 2\pi\sqrt{\frac{l}{g}}$$

En mesurant la longueur du pendule et sa période, donc deux mesures, on peut en déduire l'intensité de la pesanteur

$$g = l\times\frac{4\pi^2}{T^2}$$

En déduire l'expression de $\Delta g$

  • Dans une expérience d'optique on mesure l'interfrange $i$ dans une figure d’interférences
$$i = \frac{\lambda\, D}{a}$$

$\lambda = 567 \pm 1\,\text{nm}\quad D = 2,23 \pm 0,005\,\text{m}\quad a=100 \pm 1\,\mu\text{m}$

Déterminer pour un niveau de confiance de $95\%$ la mesure $i = i_m \pm \Delta i_m$

  • On cherche à déterminer la puissance dissipée par effet Joule dans une résistance $R$ sachant que l’on a mesuré l'intensité $I$ circulant dans la résistance et la résistance elle-même ($P=RI^2$). Les deux mesures donnent les résultats suivants :

$R = 23,4 \pm 0,2\,\Omega\quad I = 0,375 \pm 0,001\,\text{A}$

Déterminer pour un niveau de confiance de $95\%$ la mesure $P = P_m \pm \Delta P_m$

Définition de l'espérance d'une variable aléatoire (Pour en savoir plus)¶

L’espérance d’une variable aléatoire discrète $X$ dont les valeurs possibles sont $x_1, x_2,\dots, x_n$ est, lorsqu’elle existe, la somme des valeurs prises par cette variable, pondérées par leurs probabilités de réalisation.

$$E(X) = \sum\limits_{i=1}^n x_iP(X=x_i)$$

Remarque : Dans le cas particulier ou toutes les probabilités sont égales, l'expression prend la forme de la moyenne arithmétique.

Exemple:

Considérons une loterie dont les gains seraient attribués en fonction de la roue suivante :

La somme que l'on peut gagner est une variable aléatoire $X$ de loi de probabilité :

$$ \begin{array}{c|c|c|c} X_i & 0 & 50 & 100 \\\hline P_i & \dfrac{7}{10} & \dfrac{2}{10} & \dfrac{1}{10}\\ \end{array} $$

L'espérance notée $E(X)$ de la variable aléatoire $X$ sera : $E(X) = 0\times\dfrac{7}{10} + 50\times\dfrac{2}{10} + 100\times\dfrac{1}{10} = 20$

L’espérance des gains est de 20 euros par partie, si la mise est nulle. Par conséquent si la mise est inférieure à 20 euros, il est conseillé de jouer à l'infini. Par contre si la mise est de exactement 20 euros, l'espérance des gains est de 0.

La moyenne arithmétique d'une distribution¶

Définiton de la moyenne d'échantillonnage

Pour des échantillons de taille n, la moyenne d'échantillonnage est donnée par : $$\overline{X} = \dfrac{1}{n}\sum\limits_{i=1}^{n}x_i$$

Dispersion d'une distribution¶

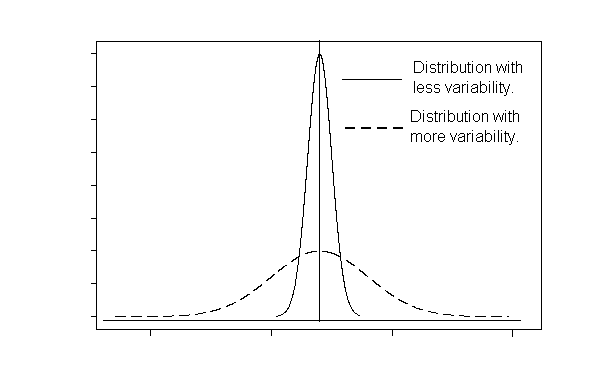
La variance et l'écart-type mesurent eux la dispersion des mesures autour de la moyenne (ou espérance).

Variance

$$ \begin{align} V(X) &=E[(X - E(X)^2]\\ &\\ &=\sum\limits_{i=1}^{n} P(X=x_i)(x_i-E(X))^2\\ &\\ &=\sum\limits_{i=1}^{n} P(X=x_i)(x_i-\overline{X})^2\\ &\\ &= \frac{1}{n}\sum\limits_{i=1}^{n} (x_i-\overline{X})^2 \quad\quad\text{(si toutes les probabilités sont équivalentes)} \end{align} $$

La variance est une mesure de la dispersion (ou de la distribution) des valeurs de la variable aléatoire autour de la moyenne. Si les valeurs tendent à se concentrer au voisinage de la moyenne la variance est faible tandis que si les valeurs tendent à se disperser plus loin la variance est grande.

Écart type¶

$$\sigma(X) = \sqrt{V(X)}$$
In [12]:
import numpy as np
import scipy.stats as stat 
echantillon = np.array([2., 3., 6., 8., 11.])
print(np.mean(echantillon))    #moyenne
print(np.std(echantillon))     #écart-type
print(stat.describe(echantillon))  #dénominateur en N-1 ?

6.0
10.8
(5, (2.0, 11.0), 6.0, 13.5, 0.236670240897294, -1.3230452674897122)
  • Nombre d'échantillons = 5
  • (min, max) = (2, 11)
  • Moyenne = 6.0
  • Variance = 13.5
In [11]:
In [ ]: