Devoir sur table : Matrices¶

1. Compléter les étoiles de la formule donnant les coefficients de $A\times B$, $A = (a_{ik})_{ \begin{array}{c}1\leq i\leq *\\1\leq k\leq * \end{array}}$ une matrice de $\mathcal{M}_{*,*}(\mathbb{K})$ et $B = (b_{kj})_{ \begin{array}{c}1\leq k\leq *\\1\leq j\leq * \end{array}}$ une matrice de $\mathcal{M}_{*,*}(\mathbb{K})$

2. Calculer si possible le produit $A\times B$ et $B\times A$:

$$ A = \begin{pmatrix} -2 & 1 & 0\\ 1 & 4 & 1\\ -3 & -1 & 0\end{pmatrix} \quad B = \begin{pmatrix} 1 & -1\\ 0 & -2 \\ 1 & -3\end{pmatrix}$$

3. Déterminer si les énoncés suivants sont vrais ou faux (dans ce cas donner un contre exemple pour justifier), $n\in \mathbb{N}$ et $n>2$

  1. Si $A$ et $B\in \mathcal{M_n}(\mathbb{K})$, $A\times B = B\times A$
  2. On peut trouver deux matrices $A$ et $B$ non nulles dans $\mathcal{M_n}(\mathbb{K})$ telles que $A\times B = 0$
  3. Si $A\times C = B\times C$, avec $C$ non nulle, alors $A=B$
  4. On peut trouver une matrice $A$ non nulle dans $\mathcal{M_n}(\mathbb{K})$ telle que $A^n = 0$

4. Déterminer l'inverse de la matrice (justifier que le calcul de l'inverse est possible): $A = \begin{pmatrix} 1 & 0 & -1\\ 2 & 1 & -3\\ -1 & 0 & 2\end{pmatrix}$

En déduire les solutions du système :
$$A\begin{pmatrix} x\\ y\\ z\end{pmatrix} = \begin{pmatrix} 1\\ 2\\ 3\end{pmatrix}$$

5. Soit le graphe suivant :

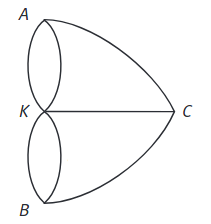
  1. Donner la matrice d'adjacence $M$ associée ce graphe
  2. Calculer les matrices $M^2$ et $M^3$
  3. En déduire : 
     a. le nombre de chaînes de longueur 2 permettant d'aller de C à C et de C à K
 b. le nombre total de chaînes de longueur 3 permettant d'aller d'un point quelconque vers lui même.

6. Sur le tableau de notes d'un concours vous lisez les notes et les moyennes suivantes:

$$ \begin{array}{ccccc} \text{Candidats} & \text{Informatique} & \text{Mathématiques} & \text{Physique} & \text{Moyennes}\\ X_1 & 7 & 12 & 8 & 9\\ X_2 & 9 & 6 & 10 & 8.6\\ X_3 & 11 & 16 & 14 & 14\\ \end{array} $$

En déduire les coefficients de chaque matière

Christophe Casseau ENSAM 2017-2018, Bachelor 2

In [5]:
import numpy as np
M = np.array([[0, 0, 1, 2],[0, 0, 1, 2],[1, 1, 0, 1],[2, 2, 1, 0]])
M2 = np.dot(M, M)
M3 = np.dot(M2, M)
print(M2)
print
print(M3)

[[5 5 2 1]
 [5 5 2 1]
 [2 2 3 4]
 [1 1 4 9]]

[[ 4  4 11 22]
 [ 4  4 11 22]
 [11 11  8 11]
 [22 22 11  8]]
In [7]:
A = np.array([[1, 0, -1],[2, 1, -3],[-1, 0, 2]])
inv_A = np.linalg.inv(A)
print(inv_A)
print
B = np.array([[1],[2],[3]])
X = np.dot(inv_A, B)
print X

[[ 2.  0.  1.]
 [-1.  1.  1.]
 [ 1.  0.  1.]]

[[ 5.]
 [ 4.]
 [ 4.]]
In [ ]: