INTRODUCTION À L'ANALYSE NUMÉRIQUE¶
Résolution d'équations du type $f(x)=0$¶
Introduction¶
Nous allons nous intéresser aux équations à une variable réelle de la forme $f(x)=0$ où $f$ est une fonction donnée à valeurs dans $\mathbb{R}$
Chercher la ou les solutions de l'équation $f(x) = 0$ revient à chercher la ou les solutions de l'équation $f(x) + x = x$.
En posant $g(x) = f(x) + x$ il est donc équivalent de s'intéresser aux solutions de l'équation $g(x)=x$ appelée problème du point fixe
Deux approches différentes à utiliser selon le contexte.
Remarque importante : Il n'existe pas de formule générale (a part quelques cas particuliers comme les polynômes de degré inférieur ou égal à 4) permettant de trouver la ou les solutions d'une équation du type $f(x) = 0$, pour une fonction $f$ quelconque.
Quelques définitions¶
Zéro d'une fonction¶
Définition 1 : On appelle zéro d'une application $\ f\,:\,E \rightarrow \mathbb{R}\ $ tout $x_r\in\ E$ vérifiant $\ f(x_r)=0$
Exemples
Point fixe d'une fonction¶
Définition 2 : On appelle point fixe d'une application $\ g\,:\,E \rightarrow \mathbb{R}\ $ tout $x_r\in\ E$ vérifiant $\ g(x_r) = x_r$
Exemples
Représentation graphique des solutions¶
Soit l'application $\ f : x\mapsto \dfrac{1}{x}\sin\left(\dfrac{\pi}{x}\right)$
Les zéros la fonction $f$ sur l'intervalle [0.05 ; 0.2] correspondent à l'intersection de la courbe représentative de $f$ avec l'axe $Ox$
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def f(x):
return 1/x*np.sin(np.pi/x)
x = np.linspace(0.05, 0.2, 300)
y = f(x)
plt.grid()
plt.plot(x, y)
plt.show()
Soit l'application $\ f : x\mapsto x^2 - 2x - 3$
Les point fixes de la fonction $g$ qui sont donc les solutions de $g(x) = x$ sont aussi la ou les intersections de la courbe représentative de $g$ avec la courbe représentative de $h$ encore appelée première bissectrice.
def f(x):
return x**2 - 2*x -3 # les zéros sont -1 et 3
def g(x):
return f(x) + x
x = np.linspace(-6, 6, 300)
yf = f(x)
yg = g(x)
plt.figure(num=None, figsize=(8, 6), dpi=80, facecolor='w', edgecolor='k')
plt.xticks(np.arange(-6, 7, step=1))
plt.yticks(np.arange(-6, 10, step=1))
plt.grid()
plt.ylim(-6, 10)
plt.plot(-1, 0, 'o')
plt.plot(3, 0, 'o')
plt.plot(x, yf, 'b-', label='$f(x) = x^2-2x-3$')
plt.plot(x, yg, 'r--', label="$g(x) =f(x)+x$")
plt.plot(x, x, 'g', label='$h(x) = x$')
plt.legend(loc='upper center', shadow=True, fontsize='x-large')
plt.show()
Méthodes numériques¶
Sur quoi vont s'appuyer les méthodes de résolution numériques ?
- Une propriété des valeurs intermédiaires
- Une propriété du point fixe
Propriété des valeurs intermédiaires :
- Soient $\ a,b\in\mathbb{R}, a<\ b$
- Soit $\ f: [a, b] \rightarrow \mathbb{R}\ $ une application continue telle que $f(a)$ et $f(b)$ non nuls et de signe opposés.
Alors il existe $x_r\in]a, b[$ tel que $f(x_r)=0$, si de plus $f$ est strictement monotone alors $x_r$ est unique.
Propriété du point fixe :
- Soient $\ a,b\in\mathbb{R}, a<\ b$
- Soit $\ f: [a, b] \rightarrow \mathbb{R}\ $ une application continue telle que $g([a, b])\subset[a, b]$
Alors il existe $x_r\in[a, b]$ tel que $g(x_r) = x_r$
Preuve :
- À vous de jouer
La dichotomie¶
Principe :
Soit $x_r$ un zéro unique de $f$ dans un intervalle $[a, b]$, tel que $f(a)$ et $f(b)$ de signe opposés.
La méthode consiste à localiser $x_r$ de manière de plus en plus précise par itération successive en divisant par deux la longueur de l'intervalle à chaque itération. La méthode s'arrète quand longueur de l'intervalle est inférieure à une précision fixée dès le départ.
Cela revient à construire deux suites adjacentes $(u_n)_{n\in\mathbb{N}}$ et $(v_n)_{n\in\mathbb{N}}$ convergeant vers $x_r$
Application :
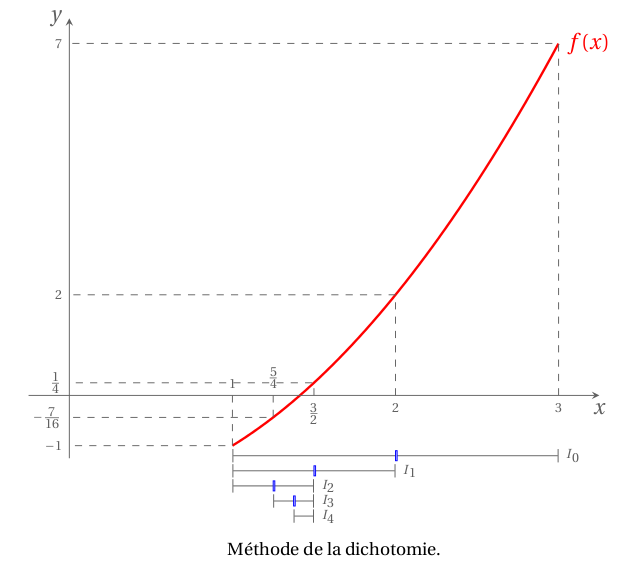
Soit une fonction $\ f : x \mapsto x^2-2\quad$ avec $\quad x\in[1,3]$.
Déterminer les trois premiers itérés avec la méthode de la dichotomie pour obtenir une valeur approchée du zéro de $f$ dans cet intervalle
Combien de pas de dichotomie doit-on effectuer pour améliorer d’un ordre de grandeur la précision de l’approximation de la racine ?
Graphiquement : image extraite d'un cours G.Faccanoni
Implémenter une fonction $dichotomie(f, a, b, epsilon)$ qui renvoie une valeur approchée d'un zéro de $f$ à $epsilon$ près dans l'intarvalle $[a, b]$
def dichotomie(f, a, b, epsilon):
'''
f : la fonction mathématique à étudier
a,b : les bornes de l'intervalle d'étude de f
epsilon : la précision sur la valeur approchée d'un zéro de f
'''
g, d = a, b
fg, fd = f(g), f(d)
while abs(d - g) > epsilon:
# À compléter
return g, d
Newton¶
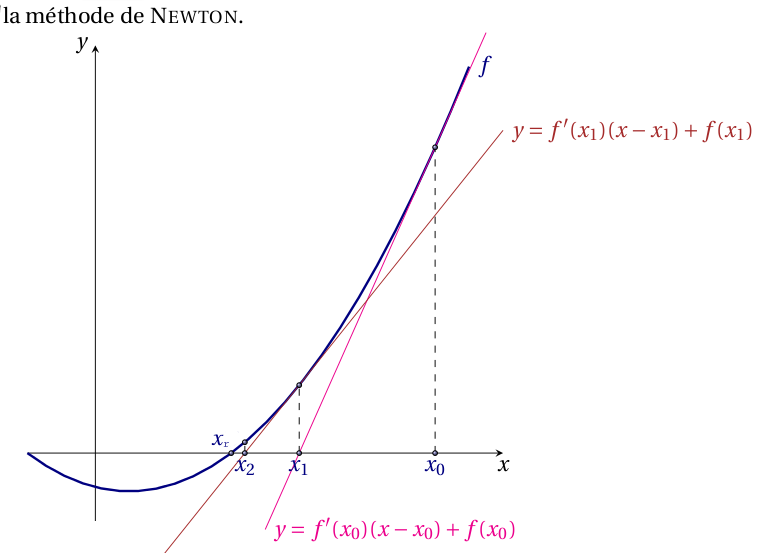
Principe :
Le principe en est le suivant : partant d'une valeur $x_0$, on trace la tangente à la courbe représentative de $f$ au point $M_0(x_0, f(x_0))$; cette droite coupe l'axe des abscisses en un point d'abscisse $x_1$:
$$x_1 = x_0-\frac{f(x_0)}{f'(x_0)}$$
Approcher un zéros de $f$ se ramène donc à considérer la suite récurrente définie par une valeur de départ $u_0$ proche de la racine $x_r$ et par la relation :
$$u_{n+1} = u_n-\frac{f(u_n)}{f'(u_n)}$$
On considère que la fonction $f'$ ne s'annule pas sur [a, b] et que si $u_0$ est assez proche de $x_r$ alors la suite $(u_n)_{n\in \mathbb{N}}$ converge vers $x_r$, malheureusement il est difficile de savoir en pratique si on est assez proche de $x_r$.
Graphiquement : image extraite d'un cours G.Faccanoni
Application :
Soit une fonction $\ f : x \mapsto x^2-2\quad$ avec $\quad x\in[1,3]$.
- Déterminer les trois premiers itérés avec la méthode de Newton pour obtenir une valeur approchée du zéro de $f$ avec $x_0 = 2$
Implémenter une fonction $newton(f, g, a, epsilon)$ qui renvoie une valeur approchée d'un zéro de $f$ à $epsilon$ près.
def newton(f, g, a, epsilon):
'''
f : la fonction mathématique à étudier
g : la dérivée de la fonction f
epsilon : la précision sur la valeur approchée d'un zéro de f
'''
x = a # Premier terme de la suite récurrente x0
y = x - f(x)/g(x) # On calcule x(n+1)
while abs(y-x)>epsilon: # Critère d'arrêt |x(n+1) - x(n) < epsilon|
# A compléter
return y
Utilisation de numpy / scipy¶
from scipy import optimize
- $numpy.roots$ détermine les racines d'un polynôme donné par la liste de ces coefficients, pour le polynôme $P(X)=X^2-2$ on a :
np.roots([1, 0, -2])
- $scipy.optimize.bisect$ une implémentation de la méthode de dichotomie
optimize.bisect(lambda x: x**2 - 2, 1, 3)
- $scipy.optimize.newton$ une implémentation de la méthode de Newton, à noter que si on ne donne pas la dérivée c'est la méthode de la sécante qui est utilisée.
optimize.newton(lambda x: x**2 - 2, 2)
Conclusion¶
Il n'y a pas vraiment de méthode universelle de résolution pour une équation du type $f(x)=0$, chaque méthode a ses avantages et ses inconvénients dont il faut être conscient. Le choix sera fait en fonction des besoins: rapidité, connaissance de $f'$ et/ou $f"$, d'une bonne approximation d'un zéro, etc. On peut pratiquer des méthodes mixtes avec une première phase de dichotomie pour approcher grossièrement un zéro puis Newton pour affiner le résultat.
Résolution numérique approchée d'une équation différentielle ordinaire¶
Dans cette partie on cherche à confronter une méthode de résolution numérique des équations différentielles à valeurs réelles et pour fixer les idées, on suppose que la variable d’intégration des équations différentielles considérées est le temps t. L' équation linéaire non homogène à coefficients constants suivante :
$$(E)\quad ay'(t) + by(t) = \gamma(t) \quad\text{avec}\quad a \neq 0$$
équivaut à :
$$(E)\quad y'(t) = -\frac{b}{a}y(t) + \frac{\gamma(t)}{a}$$
Cette transformation s’applique à toute équation différentielle linéaire, quel que soit son ordre, si de plus on possède une condition initiale, soit $x_0$ un point de I, et soit $y_0$ un élément quelconque de $\mathbb{R}$. Il existe une unique solution de (E) sur I satisfaisant à la condition initiale $y(t_0) = y_0$. Trouver cette solution, c’est résoudre le problème de Cauchy relatif à ces conditions initiales. Les courbes représentatives des solutions de (E) sont appelées courbes intégrales de (E). En d'autres termes par tout point $M (x_0, y_0)$ de $I\times \mathbb{R}$, il passe une et une seule courbe intégrale de (E). On appelle forme canonique du problème de Cauchy l'écriture de l'équation différentielle sous la forme suivante :
\begin{equation} \text{Soit }T\in\mathbb{R}^+\quad \left\{\begin{aligned} &\forall t\in [0,T],\,y'(t) = f(t, y(t))\\ & y(t_0) = y_0\\ \end{aligned}\right. \end{equation}
Exemple n°1 :
Pour s'entraîner prenons une équation différentielle linéaire (scalaire) du premier ordre à coefficients constants dont on connait la forme de la solution.
La décroissance radioactive conduit à ce type d'équation différentielle:
\begin{equation} N'(t) + \lambda N(t) = 0 \end{equation}
- Mettre cette équation différentielle sous la forme d'un problème de Cauchy.
- En déduire l'expression de $f(t, y(t))$
Exemple n°2 :
Considérons l'équation différentielle linéaire du premier ordre à coefficients constants avec second membre suivante:
\begin{equation} \left\{\begin{aligned} \tau x'(t) + x(t) &= u\\ x(0) &= 0\\ \end{aligned}\right. \end{equation}
Cette équation différentielle très simple peut correspondre aux modèles physiques suivants
- charge d'un circuit RC
- montée en température d'un système thermique
- évolution de la vitesse d'un solide avec frottements
- Écrire l'equation différentielle d'un circuit RC sous la forme canonique d'un problème de Cauchy
- Identifier $f(x(t),t)$
Un module Python pour résoudre les équations différentielles: scipy.integrate.odeint¶
Dans le domaine de l'analyse numérique Python propose de nombreux modules. Les fonctions de ces modules sont en général bien mieux optimisées que les fonctions maisons. Pour les équations différentielles Python possède le solver générique assez sophistiqué: $odeint$ contenu dans le module $scipy.integrate$. À importer en début de programme
from scipy.integrate import odeint
Il résout, en autre, avec une syntaxe relativement simple les équations différentielles du type : $y' = f(y(t), t)$, avec une condition initiale.
Utilisation de scipy.integrate.odeint
Pour utiliser odeint, il faut commencer par implémenter la fonction dérivée $f(x(t),t)$ que l'on tire de la forme canonique du problème de Cauchy. Cette fonction est ensuite passée en paramètre à $odeint$ avec la condition initiale $x(t_0)$ et $t$ une list python ou un ndarray numpy pour chaque point du temps.
def f(y, t):
''' fonction scalaire de l'équation
différentielle'''
return -6e-2 * y
t = np.linspace(0, 100)
No = 8e24
x_ode = odeint(f, No, t)
plt.plot(t, x_ode, '--',label='odeint')
plt.legend(loc='upper right')
Donner une solution numérique approchée à l'exemple n°2 dans le cas d'un circuit RC avec les valeurs suivantes : $u = 2\ V$ et $\tau = 10\ s$
Transformation d'une équation différentielle du second ordre en système différentiel¶
Pour une équation différentielle linéaire homogène d’ordre 2 du type:
$$a(t)y'' + b(t)y' + c(t)y = 0$$
on pose $z_1 = y\quad\quad$ et $\quad z_2 = y'$
alors $\quad\dfrac{dz_1}{dt}=z_2\quad$ et $\quad\dfrac{dz_2}{dt}=-\dfrac{b(t)z_2 + c(t)z_1}{a(t)}$
Nous obtenons donc un système de deux équations différentielles d'ordre 1 à résoudre :
$$\begin{pmatrix} \dfrac{dz_1}{dt}\\ \dfrac{dz_2}{dt} \end{pmatrix} = \begin{pmatrix} z_2\\ -\dfrac{b(t)z_2 + c(t)z_1}{a(t)} \end{pmatrix} $$
Remarques : On procède de même pour les ED d’ordre 2 non homogènes. La transformation précédente s’applique à toute équation différentielle linéaire, quel que soit son ordre voir à certaines équations non-linéaires comme celle du pendule simple.
Application au pendule simple¶
En écrivant la relation fondamentale de la dynamique, on obtient l’équation du pendule simple (absence de frottements) donnée par
$$\theta'' + \omega^2\, \sin(\theta) = 0$$
où $\theta$ est l’angle du pendule par rapport à la verticale et $\omega = 3\ \text{rad/s}$.
- Écrire le système différentiel correspondant à cette équation différentielle.
def pend(y, t):
'''
Fonction décrivant le système ED étudié, renvoie l'évolution du système à un instant donné
y : la liste contenant les variables fonction du temps dans y' = f(x(t), t)
t : instant donné
omega : constante du problème
'''
theta, z2 = y
dydt = [z2, -omega**2*np.sin(theta)]
return dydt
# définition de l’intervalle de temps
t0 = 0
tmax = 15
npoints = 1000
temps = np.linspace( t0 , tmax , npoints)
# Les conditions initales
cond_init = [np.pi/3, 0] # theta_zero (rad) et theta_point_zero (rad/s)
# les constantes
omega = 3
# La résolution du système
y_ode = odeint(pend, cond_init, temps)
# Le graphique
plt.plot(temps, y_ode[:, 0], 'b', label="$\theta(t)$")
plt.plot(temps, y_ode[:, 1], 'g', label="$\theta'(t)$")
plt.grid()
plt.show()
Application au pendule simple amorti¶
$$\theta'' = -\frac{g}{L}\,\sin(\theta) - \lambda\,\theta'$$
Quel changement de variables doit-on poser pour obtenir le système différentiel suivant ?
- Le système différentiel
$$\begin{pmatrix} z'_1\\ z'_2 \end{pmatrix} = \begin{pmatrix} z_2\\ -\dfrac{g}{L}\,sin(z_1) - \lambda\, z_2 \end{pmatrix} $$
- Conditions initiales
$$\theta'(t_0)=0 \quad\text{et}\quad\theta(t_0)=\frac{\pi}{2}$$
Tracer graphiquement une solution numérique approchée du système
Christophe Casseau BA3 ENSAM