Dérivation - Intégration¶
from sympy import *
init_printing(use_unicode=True) #affichage à la LaTeX
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
Motivation¶
- Étude du comportement d'une fonction
- Application à des fonctions issues de problèmes liés à la physique
- Cinématique
- Électrocinétique
- Cinétique chimique
Notion de fonction continue¶
- Dans la suite de ce chapitre, on considère essentiellement des fonctions numériques définies sur un intervalle $I$ non vide et non réduit à un point (on dit aussi intervalle d’intérieur non vide).
- Les fonctions usuelles (fonctions puissances, trigonométriques, exponentielle, logarithme, etc.) sont continues sur leur domaine.
- Les deux proprités suivantes permettent d’affirmer la continuité d’une fonction numérique définie comme des opérations sur des fonctions usuelles.
Propriété : sommes, produits et quotients de fonctions continues
- Soit $f$ et $g$ deux fonctions continues sur l’intervalle I. Alors les fonctions $\alpha f + \beta g$ et $fg$ sont continues sur I.
- Si $g$ ne s’annule pas sur $I$, alors les fonctions $\dfrac{1}{g}$ et $\dfrac{f}{g}$ sont continues sur $I$.
Propriété : composée de deux fonctions continues
Soit $f : I \rightarrow \mathbb{R}$ et $g : J \rightarrow \mathbb{R}$ deux fonctions continues, avec $f(I) \subset J$.
Alors la fonction $g\circ f$ est continue sur $I$.
Notion de dérivée¶
Soit $f : I\rightarrow \mathbb{R}$ et $a\in I$, on cherche un procédé pour étudier le comportement (variation) de $f$.
On veut fabriquer un outil, une nouvelle fonction, que l’on notera $f'$, qui nous donnera des informations sur la fonction initiale $f$.
- On dit que $f$ est dérivable en $x_0$ si l'expression $\dfrac{f(x)-f(x_0)}{x-x_0}$ possède une limite finie quand $x$ tend vers $x_0$ ou si $\dfrac{f(x_0+h)-f(x_0)}{h}$ possède une limite finie quand $h$ tend vers $0$
- Cette limite est alors notée $f'(x_0)$ et est appelée nombre dérivée de $f$ en $x_0$ aussi noté : $\dfrac{d\,f}{dx}(x_0)$
- Si $f$ est dérivable en tout point $x_0\in I$, on dit que $f$ est dérivable sur I et on note $f'$ la dérivée de $f$
- Si $f$ est dérivable en $x_0$, on appelle tangente à $(\mathcal{C})$ en $x_0$ la droite d'équation $y-f(x_0) = f'(x_0)(x-x_0)$ de coefficient directeur $f'(x_0)$ et qui passe par le point $A(x_0, f(x_0))$ de la courbe $(\mathcal{C})$
Équation de la tangente en un point¶
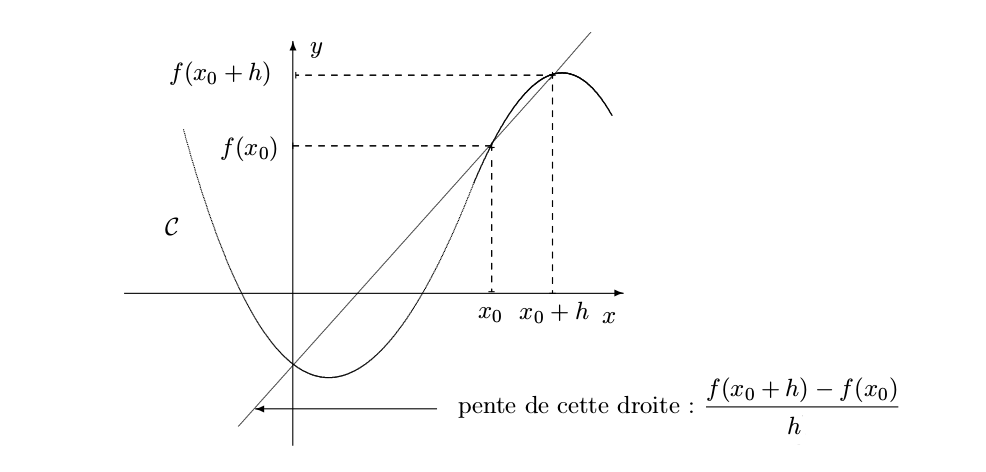
Il existe des fonctions pour lesquelles, la limite précédente n’existe pas. On dit qu’elles ne sont pas dérivables en $x_0$
- $f(x) = \sqrt x$ en $0$
- $f(x) = |\,x\,|$ en $0$
Comprendre le sens physique de la dérivée en un point¶
- Donne une information sur la vitesse au voisinage d'un point de la trajectoire d'un solide, la vitesse correspond à la variation de la distance parcourue en fonction du temps $$v = \dfrac{dx}{dt}$$
- En cinématique du solide l'accélération est donnée par la variation de la vitesse en fonction du temps $$a = \dfrac{dv}{dt}$$
- En électromagnétisme la fem induite induite dans un circuit fermé baigné par un champ magnétique est directement proportionnelle à la variation dans le temps du flux du champ magnétique pénétrant dans le circuit. $$E = \dfrac{d\Phi_B}{dt}$$
- En cinétique chimique la vitesse $v$ de la réaction chimique est donnée par la variation de la concentration en fonction du temps des différents réactifs et produits. $$v = -\dfrac{d[A]}{dt} = -\dfrac{d[B]}{dt} = \dots$$
Pour chaque grandeur physique citée, la connaissance de l'évolution de cette grandeur en fonction du temps permet d'exprimer le taux de variation de cette grandeur en un point et d'en déduire une information liée à la notion de dérivée.
Opérations sur les fonctions dérivables¶
Propriété : dérivée d'une combinaison linéaire
Soient $f$ et $g$ deux fonctions dérivables sur un intervalle $I$.
Pour tout $\alpha$, $\beta$ dans $\mathbb{R}$, $h = \alpha\,f + \beta\, g$ est dérivable sur $I$ et $h' = \alpha\,f' + \beta\, g'$
Propriété : dérivée d'un produit
Soient $f$ et $g$ deux fonctions dérivables sur un intervalle $I$.
La fonction $h = f\,g$ est dérivable sur $I$ et $h' = f' g + f\,g'$
Propriété : dérivée de l'inverse et du quotient
Soit $g$ une fonction dérivable sur un intervalle $I$ et ne s'annulant pas sur $I$.
La fonction $h = \dfrac{1}{g}$ est dérivable sur $I$ et $h' = -\dfrac{g'}{g^2}$
Soit $g$ une fonction dérivable sur un intervalle $I$
La fonction $h = \dfrac{f}{g}$ est dérivable sur $I$ et $h' = \dfrac{f'g - f\,g'}{g^2}$
Propriété : dérivée d'une composée
Soient $f : I \rightarrow \mathbb{R}$ et $g : J \rightarrow \mathbb{R}$ deux fonctions dérivables avec $f(I)\subset J$.
La fonction $h = g\circ f$ est dérivable sur $I$ et $h' = f'\times (g'\circ f)$
C'est à dire que $\forall x\in I,\,(g\circ f)'(x) = g'(\,f(x)\,)\times f'(x)$
Exercices : Donner le domaine de dérivabilité ainsi que la dérivée des fonctions suivantes :
- $h : x \mapsto \sqrt{x^2 + 2x -3}$ (Vérifier que $f$ n'est pas dérivable en 1)
- $h : x \mapsto \cos(\dfrac{1}{x})$
- $h : x \mapsto \sqrt{\dfrac{x+1}{x-1}}$
- $h : x \mapsto \ln(1+\sqrt{1+e^{2x}})$
- $h : x \mapsto x^{x^2}$
- $h : x \mapsto \ln(1 + 2\sqrt{2\sin(x)+1})$
Calcul symbolique avec Python et sympy¶
from sympy import *
Variable symbolique¶
La fonction Symbol de SymPy permet de créer une variable symbolique:
x = Symbol("x")
x+x+2*x
Expression formelle de la dérivée¶
our dériver une fonction par rapport à une variable $x$, on utilise la fonction diff de sympy avec la syntaxe :
$$\text{diff(fonction, x)}$$diff(log(1+sqrt(1+exp(2*x))),x)
Dérivée seconde, concavité, inflexions¶
Même si la dérivée première donne beaucoup d'informations à propos d'une fonction, elle ne la caractérise pas complètement. pour obtenir des informations supplémentaires nous pouvons utiliser la dérivée seconde de la fonction.
Définition
Soit $f : I \rightarrow \mathbb{R}$ une fonction numérique dérivable sur un intervalle I.
Si $f$ est dérivable sur $I$, on dit que $f$ est deux fois dérivable sur $I$, et on note $f''$. On dit que $f''$ est la fonction dérivée seconde de $f$ .
Concavité¶
Définitions
- Une fonction $f$ est dite convexe sur un intervalle $I$, si pour toutes paires de points sur le graphe de $f(x)$, le segment de droite qui relie ces deux points passe au dessus de la courbe de $f(x)$.
- Une fonction $f$ est dite concave sur un intervalle $I$, si pour toutes paires de points sur le graphe de $f(x)$, le segment de droite qui relie ces deux points passe au dessous de la courbe de $f(x)$.
Propriété :
Soit $f : I \rightarrow \mathbb{R}$ une fonction numérique deux fois dérivables sur un intervalle I.
- La fonction $f$ est convexe si $f''(x)>0$ quelque soit $x\in I$
- La fonction $f$ est concave si $f''(x)<0$ quelque soit $x\in I$
Remarque : La dérivée première donne la pente de la tangente en un point de la courbe de la fonction f et la dérivée seconde donne l'allure de la courbe de la fonction f sur un intervalle $I$
Exercices
- Étudier la courbure de la courbe : $f(x) = x^2 + 2x - 4$
- Trouver les intervalles sur lesquels la fonction $f : x \rightarrow ln(x^2+1)$ est concave
- À l'aide de Python trouver les intervalles de concavité et de convexité de la fonction $f : x\rightarrow x^4 - 2x^3 - 12x^2 + 8x + 6$
def f(x):
return np.log(x**2 + 1)
def f_2(x):
return (2 - 2*x**2)/(x**2+1)**2
x = np.linspace(-2, 2)
y = f(x)
y_2 = f_2(x)
plt.plot(x, y)
plt.plot(x, y_2)
plt.grid()
plt.show()
Inflexions¶
Soit $f : I \rightarrow \mathbb{R}$ une fonction numérique deux fois dérivables sur un intervalle I.
Si la fonction $f''$ change de signe en un point $a \in I$, cela se traduit par un changement de concavité au point $A(a, f (a))$ pour la courbe de la fonction $f$
En ce point la courbe de la fonction $f$ traverse sa tangente.
On exprime cette situation en disant que $A(a, f (a))$ est un point d’inflexion de la courbe de la fonction $f$.
Dérivées partielles, notations¶
La dérivation d’une fonction d’une variable peut être généralisée. Les dérivées partielles d’une fonction de deux variables x et y se calculent de la façon suivante :
- par rapport à x : on considère que y est constant et on dérive la fonction comme fonction d’une variable x.
- par rapport à y : on considère que x est constant et on dérive par rapport à y.
La dérivée partielle de $f$ par rapport à $x$ se note $\dfrac{\partial f}{\partial x}$, la dérivée partielle de $f$ par rapport à $y$ se note $\dfrac{\partial f}{\partial y}$
Exercices : Calculer les dérivées partielles des fonctions suivantes
- Soit $f$ une fonction définie sur $\mathbb{R}^2$ par $f(x, y) = x^2 + y^2$
- Soit $g$ une fonction définie sur $\mathbb{R}^2$ par $g(x, y) = x^3 e^y$
On rappelle la loi de Boyle Mariotte, valable pour une mole de gaz parfait : $P V = RT $, où $P$ désigne la pression du gaz, $V$ son volume, $R$ la constante des gaz parfaits et $T$ la température du milieu.
- Calculer $\dfrac{\partial P}{\partial T}$ et $\dfrac{\partial P}{\partial V}$
- Même question si l’on considère à présent la relation de Van der Waals, avec les mêmes conventions que précédemment, et avec a et b réels :
from mpl_toolkits.mplot3d import Axes3D
ax = Axes3D(plt.figure())
def f(x, y):
return x**2 + y**2
X = np.linspace(-2, 2, 100)
Y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(X, Y)
Z = f(X, Y)
ax.plot_surface(X, Y, Z)
plt.show()
ax = Axes3D(plt.figure())
def f(x, y):
return (x**3) * np.exp(x)
X = np.linspace(-1, 2, 100)
Y = np.linspace(-1, 2, 100)
X, Y = np.meshgrid(X, Y)
Z = f(X, Y)
ax.plot_surface(X, Y, Z)
plt.show()
Notion de primitive¶
Propriété : Primitive sur un intervalle
Soit $f$ une fonction de $I$ dans $\mathbb{R}$. On dit qu'une fonction $F: I \rightarrow \mathbb{R}$ est une primitive de $f$ sur $I$ si $F$ est dérivable sur $I$ et si, pour tout $x$ de $I$, on a $F'(x)=f(x)$
Propriété : Relation entre les primitives d'une même fonction
Soit $f : I \rightarrow\mathbb{R} $ est une fonction numérique, et soit $F$ une primitive de $f$ sur $I$.
Les primitives de $f$ sur $I$ est l'ensemble des fonctions {$x \mapsto F(x) + \lambda$}, avec $\lambda\in\mathbb{R}$
Primitives usuelles¶
Intégration sur un segment¶
Toutes les fonctions considérées dans ce paragraphe seront supposées continues.
Si $a$ et $b$ sont deux réels donnés $(a < b)$, et $f$ , une fonction continue sur $[a, b]$, alors $f$ admet une primitive sur $[a, b]$, notée $F$ tel que :
$$\int_a^b f(x)\,dx = F(b) - F(a)$$Comprendre le sens physique de l'intégrale d'une fonction¶
- En cinématique
Graphique tiré des notes de cours Simon Vézina en référence à Marc Séguin, Physique XXI Volume A

Propriétés sur les intégrales
- $\displaystyle\int^a_a f(x)\,dx = 0$
- $\displaystyle\int^b_a f(x)\,dx = - \displaystyle\int^a_b f(x)\,dx$
- $\displaystyle\int^b_a f(x)\,dx = \displaystyle\int^c_a f(x)\,dx + \displaystyle\int^b_c f(x)\,dx$
- $\displaystyle\int^b_a \lambda\,f(x)\,dx = \lambda\,\displaystyle\int^b_a f(x)\,dx\quad \forall\,\lambda\in\mathbb{R}$
- $\displaystyle\int^b_a (\,f(x) + g(x)\,)\,dx = \displaystyle\int^b_a f(x)\,dx + \displaystyle\int^b_a g(x)\,dx \quad\quad$ Linéarité de l'intégration
Intégration par parties¶
Propriété :
Soient $u$ et $v$, deux fonction dérivables sur un intervalle $I$, dont les dérivées sont continues sur $I$, et $a$ et $b$, deux réels de $I$. Alors :
$$\int_a^b u(x)\,v'(x)\,dx = \left[u(x)v(x) \right]_a^b - \int_a^b u'(x)\,v(x)\,dx$$Exercices : calculer les intégrales suivantes
- $\displaystyle\int_0^\frac{\pi}{2} x\sin(x)\,dx$
- $\displaystyle\int_1^x (t^2 + 2)\,\ln(t)\,dt\quad\quad$ avec $x\in\, ]1; +\infty]$
Changement de variable¶
Propriété :
Soit $f: I \rightarrow \mathbb{R}$ une fonction continue
Soit $g: J \rightarrow \mathbb{R}$ dérivable sur $J$ et sa dérivée est continue, telle que $g(J)\subset I$
Alors pour tous $a,b$ de $J$, on a $\displaystyle\int_a^b f(g(t))g'(t)\,dt = \displaystyle\int_c^d f(x)\,dx \quad$ où $\quad c=g(a)$ et $d=g(b)$
Exercices : calculer les intégrales suivantes
- $\displaystyle\int_0^\frac{\pi}{4} tan(x)\,dx$
- $\displaystyle\int_{0}^t x\sqrt{1+x^2}dx$
- $\displaystyle\int_{0}^\frac{1}{2} \sqrt{1-x^2}dx$