Génération et parcours de labyrinthe¶
Dans un premier temps l'objectif est d’écrire un programme générant un labyrinthe. Plusieurs méthodes vont être explorées. Pour simplifier les choses le labyrinthe est défini par une grille ($n\times n)\in \mathbb{N}^2$ dont les cases peuvent être pleines (mur) ou vides (couloir).
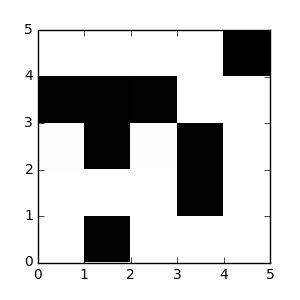
Génération aléatoire d'un labyrinthe¶
Un labyrinthe peut-être représenté à l'aide d'une matrice carrée de la forme : $\mathcal{M}_{ n,n}(\{0,1\})$ avec $n\in \mathbb{N^*}$. On décide que la valeur $1$ indique un couloir et que la valeur $0$ indique un mur. Par exemple le labyrinthe précédent peut être représenté à l'aide d'une matrice de dimension $(5\times 5)$:
Les modules à utiliser¶
import matplotlib.pyplot as plt
import matplotlib as mpl
from random import *
%matplotlib inline
Question : Détailler précisemment en quelques phrases la signification de ces quatre instructions. Vous insisterez sur les différences entre package et module et vous expliquerez la notion d'alias
Labyrinthe naïf¶
Une technique naïve de génération de labyrinthe est décrite par l’algorithme ci-dessous. Elle a pour principal mérite d’illustrer le fait que l’on va construire un labyrinthe en partant d’une matrice simulant un espace entièrement vide ne contenant que des 1 (couloir) et en ajustant aléatoirement certains coefficients à 0 pour la création d'un mur. Son défaut majeur est que le choix purement aléatoire du prochain mur à construire aboutit presque à coup sûr à un labyrinthe qui ne possède pas forcement de solution.
Algorithme naïf:
- partir d’un labyrinthe sous la forme d’une matrice.
- tant que le labyrinthe n’a pas un aspect satisfaisant faire
- choisir une case vide de façon aléatoire
- construire un mur
- fin tant que
Générer une matrice labyrinthe aléatoirement
matrice = [] # initialisation d'une liste vide (matrice)
for i in range(3): # pour chaque ligne de la matrice
ligne = [] # une liste vide prête à recevoir les valeurs d'une ligne
for j in range(3): # pour chaque colonne de la matrice
ligne.append(randint(0, 1)) # on ajoute une valeur aléatoire à la liste référencée par ligne
matrice.append(ligne) # on ajoute une ligne complète à la matrice M
# Affichage dans le Notebook
plt.matshow(matrice, cmap='gray', interpolation='none')
plt.show()
Labyrinthe défini par un taux de remplissage¶
Une autre technique est de construire le labyrinthe sur la base d'un taux de remplissage : $p$ est un réel qui appartient à l'intervalle : $[\,0,1\,]$
Les coefficients de la matrice $\mathcal{M}_{ n,n}(\{0,1\})$ avec $n\in \mathbb{N^*}$ correspondante peuvent être définis de la manière suivante :
Soient $i$ et $j$ les lignes et les colonnes de la matrice référencée par labyrinthe
Questions :
- Écrire une fonction $creerLabyrinthe(n,p)$ dont les paramètres sont la dimension de la matrice $n\in\mathbb{N}^*$, le taux de remplissage $p\in [0, 1]$ et renvoyant une matrice labyrinthe
- Que peut-on dire du labyrinthe en fonction de la valeur $p$ ?
- Quel est son intérêt par rapport au labyrinthe naïf précédent ?
| $n=10$ , $p=0.3$ | $n=10$ , $p=0.7$ |
|---|---|
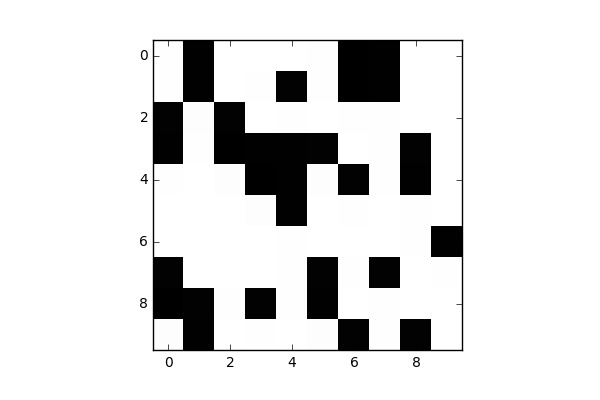 |
 |
L'affichage dans le notebook se fait ensuite de la manière suivante :
lab = creerLabyrinthe(5,0.5)
plt.matshow(lab, cmap='gray', interpolation='none')
plt.show()
Notion de percolation¶
Pour voir apparaître un phénomène de percolation, deux ingrédients sont nécessaires :
- une structure présentant des pleins et des creux,
- un agent capable d'évoluer dans cette structure.
Le labyrinthe est donc un concept tout à fait approprié au phénomène de percolation
On dit qu'il y a percolation quand l'agent qui se déplace dans les creux de la structure est capable de traverser cette dernière de part en part. Dans le cas de la machine à café, il y a effectivement percolation puisque l'eau chaude traverse la poudre de café. De nombreuses autres situations répondent au phénomène de percolation : infiltration des eaux de pluie, feux de forêt, propagation d'épidémie, etc.
Pour notre labyrinthe aléatoire, il exite un seuil $S_p$, appelé seuil critique de percolation qui est le seuil minimal pour lequel le labyrinthe possède une solution.
Pour remplir un labyrinthe par percolation, on réalise les étapes suivantes
- on crée une liste contenant les indices des cases couloirs de la première ligne supérieure du labyrinthe
- puis, tant que cette liste n’est pas vide, on effectue les opérations suivantes :
- on extrait de cette liste les indices d’une case que l’on remplit de liquide ;
- on ajoute à la liste les indices des cases voisines correspondantes à un couloir.
- L’algorithme se termine quand la liste est vide.
Questions :
- Écrire une fonction $percolation(couleur, lab)$ qui prend en paramètre la couleur de l'agent (float) introduit dans le labyrinthe, un labyrinthe et qui renvoie un labyrinthe (sans modifier celui passé en paramètre) simulant en couleur l'agent qui se déplace dans les couloirs du labyrinthe.
- Pour afficher le résultat on utilisera le code ci-dessous:
- Écrire une fonction $isPercole(lab)$ qui prend en paramètre un labyrinthe et qui renvoie un boooléen True si la percolation est réussie et False dans le cas contraire. Par définition la percolation est réussie lorsque l'agent infiltrant atteint une case cible. Par exemple si l'agent est introduit par le haut de la structure alors une case cible est une des cases de la ligne du bas.
# début definition couleurs
couleurs = (['black', 'white', 'yellow'], [0, 1, 2, 3])
cmap = mpl.colors.ListedColormap(couleurs[0])
bounds = couleurs[1]
norm = mpl.colors.BoundaryNorm(bounds, cmap.N)
# fin définition couleurs
lab_percole = percolation(couleurs[1][-1], lab)
plt.matshow(lab_percole, interpolation='none',cmap=cmap, norm=norm )
plt.savefig("lab_percole.jpg")
plt.show()
| isPercole(lab) renvoie False : | isPercole(lab) renvoie True : |
|---|---|
 |
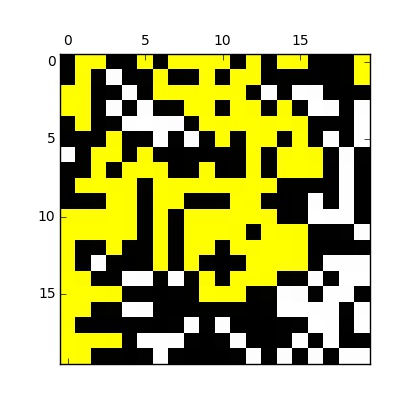 |
Seuil critique de percolation¶
Dimension de la matrice :
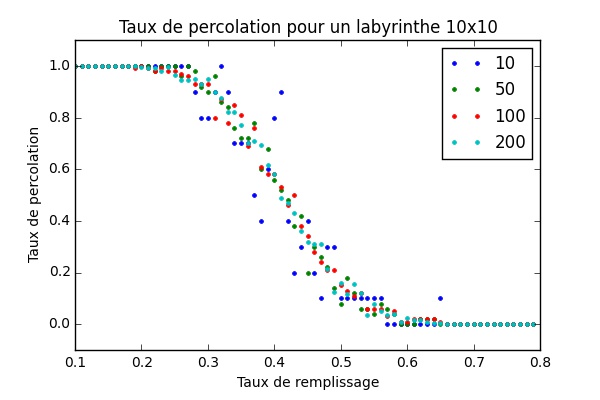
Écrire un script permettant de mettre en relation le taux de remplissage et le taux de percolation en fonction de la dimension de la matrice labyrinthe. On fixera le nombre de labyrinthes étudié à 20 (vous pouvez augmenter cette valeur si votre ordinateur est suffisamment puissant) pour une dimension donnée de la matrice labyrinthe.
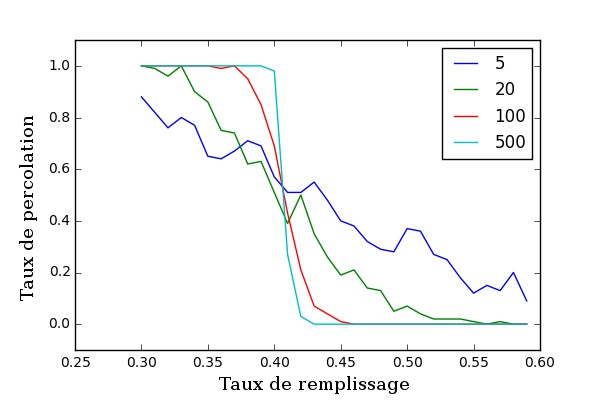
Nombre de répétitions nécessaires
Pour une dimension donnée de la matrice combien de répétitions (nombre de labyrinthe généré) sont nécessaires pour déterminer efficacement le taux de remplissage afin d'obtenir percolation ?
Labyrinthe parfait¶
Définition : Un labyrinthe est dit parfait quand il n'existe qu'un seul chemin reliant deux cellules quelconques.
Algorithme
- On part d'un labyrinthe qui ne contient que des murs.
- Toutes les cases sont à faux (0).
- On choisi une case, on met son état à vrai (1).
- Ensuite on regarde quelles sont les cases voisines disponibles c'est à dire valides et dont l'état est à 0 puis on stocke leurs positions.
- S'il y a au mois une possibilité, on en choisi une au hasard, on met la case à vrai (1), tout en gardant à l'esprit que par définition il ne doit y avoir qu'un seul chemin pour arriver sur cette case.
- On recommence l'étape (4) avec la nouvelle case.
- S'il n'y en pas, on revient à la case précédente et on recommence à l'étape (4).
- Quand on est revenu à la case départ et qu'il n'y a plus de possibilité, le labyrinthe est terminé.
Questions :
- Définir les critères permettant de vérifier l'assertion : les cases voisines disponibles
- Le point de départ étant un labyrinthe constitué uniquement de mur, écrire une fonction $detruireMur(i, j, lab)$ qui prend en arguments les coordonnées du mur à détruire $(i, j)\in\mathbb{N}^2$ et le labyrinthe en cours sous la forme d'une matrice $\mathcal{M}_{ n,n}(\{0,1\})$. Cette fonction ne renvoie rien.
- Pourquoi n'est-il pas nécessaire de renvoyer le labyrinthe modifié ?
- Pour indiquer la direction dans laquelle on se déplace on utilisera une liste de l'ensemble des points cardinaux constitué de {N, E, S, O}. Affecter une étiquette à un objet de type list contenant l'ensemble de ces valeurs. On utilisera cette étiquette comme variable globale
- Quel est l'intérêt d'une variable globale ? Donner un exemple d'une variable qui ne serait pas globale.
- Écrire une fonction $move(i, j, d)$ qui prend en argument la position actuelle $(i, j) \in \mathbb{N}^2$ dans le labyrinthe, la direction ($d$ -> str) dans laquelle on veut se déplacer et qui renvoie les coordonnées de la case d'arrivée sous la forme d'un tuple.
- move(1, 3, "E") renvoie (2, 3)
- move(1, 3, "S") renvoie (1, 4)
- Écrire une fonction $creerLabyrintheParfait(n, coups)$ qui prend en paramètres la dimension $n>2,\,n\in\mathbb{N}$ du labyrinthe et le nombre de $coups\in\mathbb{N}$ permettant de générer un labyrinthe parfait. Attention penser à diviser pour régner sur votre code, trois ou quatre fonctions seront nécéssaires.
- L'affichage du labyrinthe se fait à l'aide du code suivant :
plt.figure(figsize=(3,3)) # dimensions de l'image
lab = creerLabyrintheParfait(20, 100000)
plt.matshow(lab, cmap='gray', interpolation='none')
plt.show()

Sauvegarder un labyrinthe sous la forme d'un fichier texte¶
Mise en forme des données dans le fichier texte :
- \n : pour le retour à la ligne
- \t : pour la tabulation (la valeur par défaut est de 8), la valeur de tabulation peut être modifiée par la fonction expandtabs(val) d'un objet de type str
def saveLab(filename, lab):
fic = open(filename, "w")
for line in lab:
for c in line:
fic.write(str(c)+"\t".expandtabs(1))
fic.write("\n")
fic.close()
Génération d'un labyrinthe à partir d'un fichier texte¶
Le contenu du fichier texte lab1.txt est le suivant :
for l in open('lab1.txt'): #ouverture du fichier texte
print(l.strip()) #affichage ligne par ligne en supprimant les espaces avec la fonction : strip
def lireLabyrinthe(filename):
'''
À compléter
'''
fic = open(filename)
return[[int(i) for i in line.strip()] for line in fic]
Questions :
- Commenter de manière détaillée le code précédent (paramètre(s) de fonction, sémantique, type de retour...)
- Écrire une suite d'instructions pour afficher dans le notebook, le labyrinthe généré
import time
print time.strftime("Version du "+'%d/%m/%y %H:%M',time.localtime())
Christophe Casseau mail : isncaju@gmail.com